[GDG 스터디] 이분 그래프 (cf. BFS, DFS)

그래프와 구현 방법

그래프 ?

• 아래와 같은 자료구조를 그래프라고 한다.

 

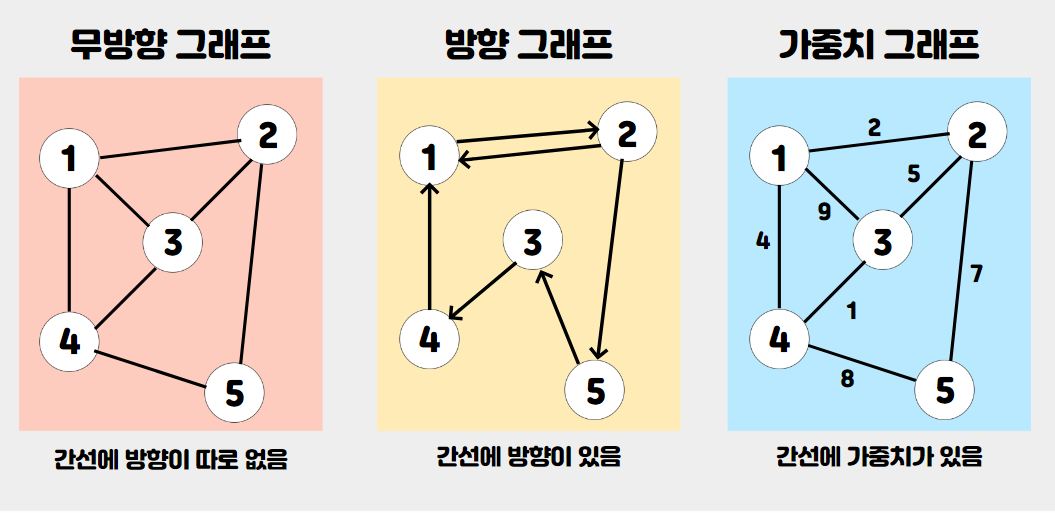
• 대표적인 구현 방식으로 3가지가 있다.
  • 엣지 리스트
  • 인접 행렬
  • 인접 리스트

---

엣지 리스트

• 이름에서 알 수 있듯이 엣지(Edge; 간선)를 중심으로 그래프를 표현한다. → 즉 그래프의 모든 간선을 리스트 형태로 저장한다 !
  • 가중치 X → 두 정점(출발지, 도착지)
  • 가중치 O → 두 정점(출발지, 도착지), 가중치

List<Edge> edgeList = new ArrayList<>();
edgeList.add(new Edge(1, 2, 5)); // 간선 (1 -> 2), 가중치 5
edgeList.add(new Edge(2, 3, 3)); // 간선 (2 -> 3), 가중치 3

• 장점
  1. 간선의 개수가 적을 때 메모리를 절약할 수 있다 !
  2. 구현이 간단하고, 특정 알고리즘(ex: 크루스칼 MST(최소 신장트리))에 적합하다.
• 단점
  1. 특정 정점과 관련된 간선을 찾으려면 모든 간선을 탐색해야 하므로 비효율적이다 !

---

인접 행렬

• 2차원 배열을 사용하여 정점 간의 연결 상태를 나타낸다 !
  • 배열의 크기는 V x V이며, V는 정점의 개수이다.
  • 간선이 있으면 배열 값은 1(또는 가중치), 없으면 0이다.

int[][] adjMatrix = new int[V][V];
adjMatrix[1][2] = 5; // 간선 (1 -> 2), 가중치 5
adjMatrix[2][3] = 3; // 간선 (2 -> 3), 가중치 3

• 장점
  1. 두 정점 간의 연결 여부를 O(1) 시간 안에 확인할 수 있다 !
  2. 구현이 간단하고 직관적이다.
• 단점
  1. 모든 정점 쌍에 대해 공간을 할당하므로, **희소 그래프(간선이 적은 그래프)**에선 메모리 낭비가 심하다.
  2. 모든 이웃을 탐색하는 데 O(V) 시간이 걸린다.

---

인접 리스트

• 각 정점에 연결된 이웃 정점들을 리스트 형태로 저장한다. → 일반적으로 배열이나 ArrayList로 구현된다.

import java.util.ArrayList;
import java.util.List;

class Main {
    public static void main(String[] args) {
        int V = 5; // 정점의 개수 (예제)
        List<List<Node>> adjList = new ArrayList<>();
        for (int i = 0; i < V; i++) {
            adjList.add(new ArrayList<>());
        }

        // 간선 추가: (1 -> 2) 가중치 5
        adjList.get(1).add(new Node(2, 5));
        // 간선 추가: (2 -> 3) 가중치 3
        adjList.get(2).add(new Node(3, 3));
    }
}

class Node {
    int vertex; // 대상 정점
    int weight; // 간선의 가중치

    // 생성자
    public Node(int vertex, int weight) {
        this.vertex = vertex;
        this.weight = weight;
    }
}

• 장점
  1. 정점에 연결된 간선만 저장하므로, 희소 그래프에서 메모리를 절약할 수 있다 !
  2. 특정 정점에 연결된 모든 이웃 정점을 효율적으로 탐색할 수 있다 !
• 단점
  1. 두 정점 간의 연결 여부를 확인하는 데 O(V) 시간이 걸릴 수 있다 ! → 이웃 탐색(BFS, DFS) 필요 !

---

어떤 방식이 효율적일까 ?

• 대부분의 경우엔 인접 리스트를 사용하는 것이 적합하다 !
  • 대부분의 그래프 문제(ex: 소셜 네트워크, 지도 경로)가 정점 수가 많고 간선이 적은 희소 그래프이기 때문에 !
  • 대부분의 **그래프 알고리즘(ex: BFS, DFS)**에서 특정 정점에 인접한 모든 이웃을 탐색하는 작업이 필요한데, 이 작업을 효율적으로 수행하기 때문에 !
• 간선이 매우 많은 경우(밀집 그래프): 인접 행렬이 유리하다. → 근데 인접 행렬을 이용하여 풀리는 문제는 인접 리스트를 사용해도 풀린다고 한다.
• 특정 알고리즘에 적합한 경우: 크루스칼의 알고리즘은 엣지 리스트가 더 효율적이다.

---

문제: 이분 그래프 (백준 1707)

문제 링크

 

---

알고리즘 [접근 방법]

• 인접 리스트로 그래프를 구현하고 BFS 혹은 DFS를 이용해서 이웃 노드가 특정 조건과 일치하는지 탐색해나간다.
• 그래프의 어떤 정점도 이웃 정점(간선으로 연결된 정점)이 같은 집합에 있지 않을 때 해당 그래프를 이분 그래프라고 한다.

---

해결 코드 1

• 이 문제를 해결하기 위한 키포인트는 두 가지인 것 같다.
  • 간선 정보를 어떻게 저장할 것인가 ?
  • 이분 그래프인지 어떻게 판별할 것인가 ?

1. while문을 통해 각각의 테스트 케이스(그래프)에 대한 정보를 인접 리스트에 저장해주고, 해당 그래프가 이분 그래프인지 탐색한다.아래처럼 정점의 번호가 1부터 시작한다는 점을 고려하지 않고 인접 리스트를 vertexCount - 1 크기로 생성해주면 어떻게 될까 ?

   ---

   for (int i = 0; i < vertexCount; i++) { // 정점 번호 → 1, … , vertexCount graph.add(new ArrayList<>());

   ---

   • ArrayList는 내부적으로 배열을 사용하고 있는 자료구조이기에, ArrayList의 유효한 인덱스 범위는 0 ~ size() - 1이다 ! → 즉, 유효한 인덱스는 0부터 vertexCount까지가 되어 인덱스를 벗어나는 문제가 발생할 수 있다 !
   ( ex: graph.get(vertexCount) → ArrayIndexOutOfBoundsException )
2. </aside>
3. }
4. <aside> 💡
5. 이분 그래프를 판별하는 기준은 다음과 같다.
   1. **방문하지 않은 노드(current)**들에 한해서 해당 노드들의 이웃 노드(neighbor)들을 BFS를 이용해 탐색한다.
   2. 현재 정점(ex: LEFT_SET)이 이웃 정점(간선으로 연결된 정점)과 같은 집합(ex: RIGHT_SET에 있는 경우, 해당 테스트 케이스는 이분 그래프가 아니다 ! → vertex[neighbor] == vertexSet[current]

• 굳이 visited 배열을 만들어 방문하지 않은 노드를 체크하는 이유는, vertexSet 배열에 0 값이 저장되어 있으면 방문하지 않은 노드라고 판단해도 되지만, 가독성을 위해 그냥 배열을 하나 만들어줬다.

import java.util.*;
import java.io.*;

public class Main {
    
    static final int LEFT_SET = -1;
    static final int RIGHT_SET = 1;
    static List<List<Integer>> graph;  // ex: 1 -> 2, 3
    static boolean[] visited;
    static int[] vertexSet;  // index: 정점 / value: 해당 정점이 속해있는 집합
    
    public static void main(String[] args) throws Exception {
        
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int testCaseCount = Integer.parseInt(br.readLine());
        StringBuilder sb = new StringBuilder();
        
        while (testCaseCount-- > 0) {
            StringTokenizer st = new StringTokenizer(br.readLine());
            int vertexCount = Integer.parseInt(st.nextToken());
            int edgeCount = Integer.parseInt(st.nextToken());
            visited = new boolean[vertexCount + 1];
            
            graph = new ArrayList<>();
            for (int i = 0; i <= vertexCount; i++) {   // 정점 번호 → 1, … , vertexCount
                graph.add(new ArrayList<>());
            }
            
            for (int i = 0; i < edgeCount; i++) {
                st = new StringTokenizer(br.readLine());
                int from = Integer.parseInt(st.nextToken());
                int to = Integer.parseInt(st.nextToken());
                
                graph.get(from).add(to);
                graph.get(to).add(from);
            }
            
            if (isBipartite(vertexCount)) {
                sb.append("YES").append("\\n");
            } else {
                sb.append("NO").append("\\n");
            }
        }
        
        System.out.print(sb.toString());
    }
    
    public static boolean isBipartite(int vertexCount) {
        vertexSet = new int[vertexCount + 1];  // 0: 미설정, 1: LEFT_SET, 2: RIGHT_SET

        for (int i = 1; i <= vertexCount; ++i) {
            if (!visited[i] && !bfsCheck(i)) {  // 아직 방문하지 않은 정점만 탐색
                return false;
            }
        }
        return true;
    }
    
    public static boolean bfsCheck(int start) {
        Queue<Integer> queue = new LinkedList<>();
        queue.add(start);
        visited[start] = true;  // 시작 정점을 방문 표시
        vertexSet[start] = LEFT_SET;
        
        while (!queue.isEmpty()) {
            int current = queue.poll(); // 현재 노드
            for (int neighbor : graph.get(current)) {
                if (!visited[neighbor]) {
                    // 이웃 노드가 아직 방문하지 않은 경우
                    visited[neighbor] = true;  // 방문 표시
                    vertexSet[neighbor] = -vertexSet[current];  // 반대 집합으로 설정
                    queue.add(neighbor);
                } else if (vertexSet[neighbor] == vertexSet[current]) {
                    // 이웃 노드가 같은 집합에 있는 경우
                    return false;
                }
            }
        }
        return true;
    }
}

---

해결 코드 2

• 위의 코드와의 차이는 이웃 노드가 같은 집합에 있는지 탐색할 때 BFS가 아닌 DFS를 이용했다는 점밖에 없다 !

import java.util.*;
import java.io.*;

public class Main {

    static final int LEFT_SET = -1;
    static final int RIGHT_SET = 1;
    static List<List<Integer>> graph;  // ex: 1 -> 2, 3
    static boolean[] visited;
    static int[] vertexSet;  // index: 정점 / value: 해당 정점이 속해있는 집합

    public static void main(String[] args) throws Exception {

        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int testCaseCount = Integer.parseInt(br.readLine());
        StringBuilder sb = new StringBuilder();

        while (testCaseCount-- > 0) {
            StringTokenizer st = new StringTokenizer(br.readLine());
            int vertexCount = Integer.parseInt(st.nextToken());
            int edgeCount = Integer.parseInt(st.nextToken());
            visited = new boolean[vertexCount + 1];

            graph = new ArrayList<>();
            for (int i = 0; i <= vertexCount; i++) {   // 정점 번호 → 1, … , vertexCount
                graph.add(new ArrayList<>());
            }

            for (int i = 0; i < edgeCount; i++) {
                st = new StringTokenizer(br.readLine());
                int from = Integer.parseInt(st.nextToken());
                int to = Integer.parseInt(st.nextToken());

                graph.get(from).add(to);
                graph.get(to).add(from);
            }

            if (isBipartite(vertexCount)) {
                sb.append("YES").append("\\n");
            } else {
                sb.append("NO").append("\\n");
            }
        }

        System.out.print(sb.toString());
    }

    public static boolean isBipartite(int vertexCount) {
        vertexSet = new int[vertexCount + 1];  // 0: 미설정, LEFT_SET, RIGHT_SET

        for (int i = 1; i <= vertexCount; ++i) {
            if (!visited[i] && !dfsCheck(i, LEFT_SET)) {  // 아직 방문하지 않은 정점만 탐색
                return false;
            }
        }
        return true;
    }

    public static boolean dfsCheck(int current, int set) {
        visited[current] = true;
        vertexSet[current] = set;

        for (int neighbor : graph.get(current)) {
            if (!visited[neighbor]) {
                // 이웃 노드를 반대 집합으로 설정하고 재귀 호출
                if (!dfsCheck(neighbor, -set)) {
                    return false;
                }
            } else if (vertexSet[neighbor] == vertexSet[current]) {
                // 이웃 노드가 같은 집합에 있는 경우
                return false;
            }
        }
        return true;
    }
}

---

정리

• 배열과 관련된 자료구조를 다룰 땐 항상 인덱스 관련한 문제가 없도록 주의하자 !
• 그래프 문제는 앞으로 마주칠 일이 많을 것이기 때문에, DFS와 BFS를 사용하는 것에 익숙해지고 문제에 따라 둘 중 더 적합한 알고리즘을 선택할 수 있는 능력을 키우도록 하자 !
• 인접 행렬을 이용하여 풀리는 문제는 인접 리스트를 사용해도 풀린다고 하니, 그래프 정보를 저장할 때엔 그냥 인접 리스트를 사용하자 !

 

https://thin-azimuth-2a9.notion.site/GDG-13cf4ee21c0080478d1af46e6d46b79c?pvs=4

GDG 스터디 - 이분 그래프 | Notion