▼ Why ?
해시 테이블을 이용하여 해결하는 알고리즘 문제를 풀기 전에, 해시 테이블이 무엇인지와 해시 함수를 통해 발생하는 충돌을 해결하는 방법에 대해 공부해보려고 한다
▼ 해시 테이블
Hash Table ?
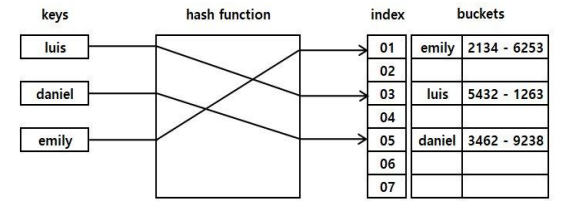
- 해시함수(Hash function)를 사용하여 키를 해시값으로 매핑하고, 이 해시값을 색인(index) 삼아 데이터의 값(value)을 키(key)와 함께 저장하는 자료구조를 "Hash table" 이라고 한다
- 이때 데이터가 저장되는 곳을 버킷(bucket) 혹은 슬롯(slot)이라고 한다
Hash Table의 시간 복잡도
- 해시테이블의 탐색, 삽입, 삭제의 시간복잡도는 평균적으로 O(1)이다
- 충돌이 빈번하게 일어나면 최악의 경우엔 O(n)의 시간복잡도로 수렴
➜ 실무에선 적재율(Load factor)이라는 것 덕분에, 해시테이블의 시간복잡도는 O(1)이라 생각한다
▼ 해시 충돌 (Hash Collision)
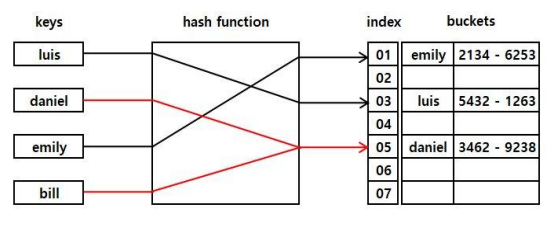
해시 충돌이 왜 발생하는가?
- 대부분의 해시함수는 해쉬값의 개수보다 많은 키값을 해쉬값으로 변환하기 때문에 해시함수가 서로 다른 두 개의 키에 대해 동일한 해시값을 내는 해시충돌(collision)이 발생
▼ 충돌 해결 방법
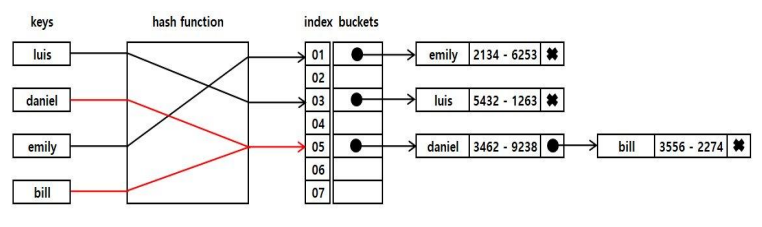
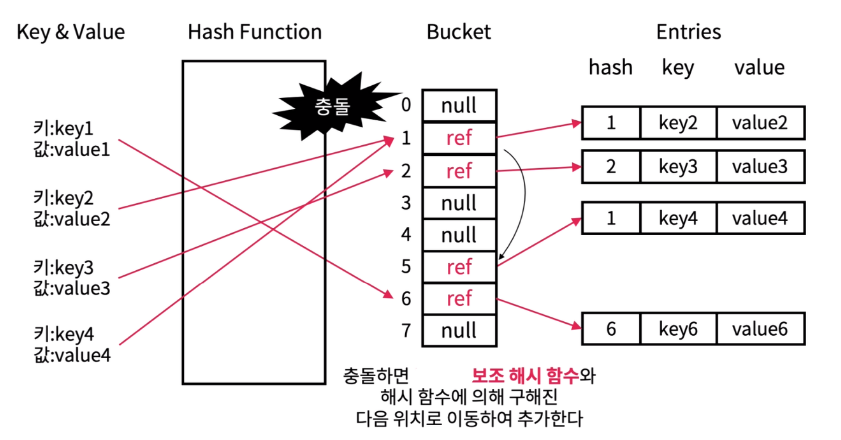
체인법 : Separate Chaining
- 한 버킷당 들어갈 수 있는 엔트리의 수에 제한을 두지 않음으로써 모든 자료를 해시테이블에 담는 것
- 해당 버킷에 데이터가 있다 체인처럼 노드를 추가하여 다음 노드를 가리키는 방식(연결리스트 : LinkedList)으로 구현하기 때문에 체인이라 한다
- 최악의 경우(Worst case)의 시간 복잡도 ➜ O(n)
- 체인법이 갖는 문제를 해결하기 위한 방법
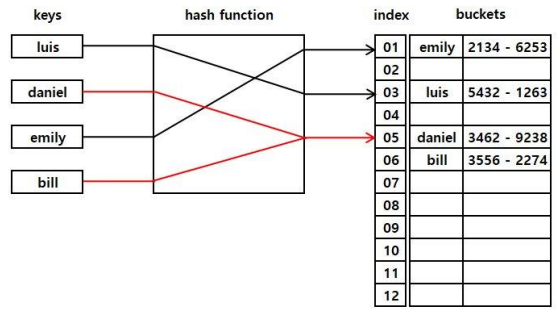
➜ 적재율에 따라 배열의 크기를 동적으로 늘리는 방식
- 적재율 (Load factor) ?
: 해시 테이블에 원소가 차 있는 비율
(ex. 해시 테이블의 전체 크기 = 100, 테이블에 저장되어 있는 원소의 개수 = 10 => 10/100 = 10%) - 실무에선 적재율(load factor)이 약 10% 정도를 유지되도록 해시테이블을 생성하고, 또 10%를 넘어가면 해시테이블을 재생성한다
➜ 따라서, 실무에선 해시테이블의 시간복잡도는 O(1)이라 생각한다.
- 적재율 (Load factor) ?
개방 번지화 : Open Addressing
- 체인법과 달리 한 버킷당 들어갈 수 있는 엔트리가 하나뿐인 해시 테이블을 사용한다
- 해시함수로 얻은 주소가 아닌 다른 주소에도 데이터를 저장할 수 있도록 허용하는 방식이다
1. 선형 탐사 (Linear probing)
- 최초 해시값에 해당하는 버킷에 다른 데이터가 저장돼 있으면 해당 해시값에서 고정 폭(보통 1칸) 만큼 옮겨 다음 해시값에 해당하는 버킷에 접근(삽입, 삭제, 탐색)합니다.
➜ 여기에 데이터가 있으면 고정 폭 만큼 또 옮겨 접근한다 - 버킷에 순차적으로 접근하다 보니 일반적인 배열과 유사한 구조를 갖게 되어 탐색이 빠르다는 해시 테이블의 장점이 사라진다 (Clustering : 군집화)
2. 제곱 탐사 (Quadratic probing)
- 최초 해시값에 해당하는 버킷에 다른 데이터가 저장돼 있으면 해당 해시값에서 그 폭이 제곱수로 늘어난다
- 임의의 키(key) 값에 해당하는 데이터에 접근할 때 충돌이 나면 1^2 칸을 옮기고, 또 충돌이 발생하면 2^2 칸을, 그 다음엔 3^3 칸을 옮기는 방식이다
- 버킷에 저장할 수 있는 공간이 있음에도 이를 찾아내지 못해 저장에 실패하는 경우 발생
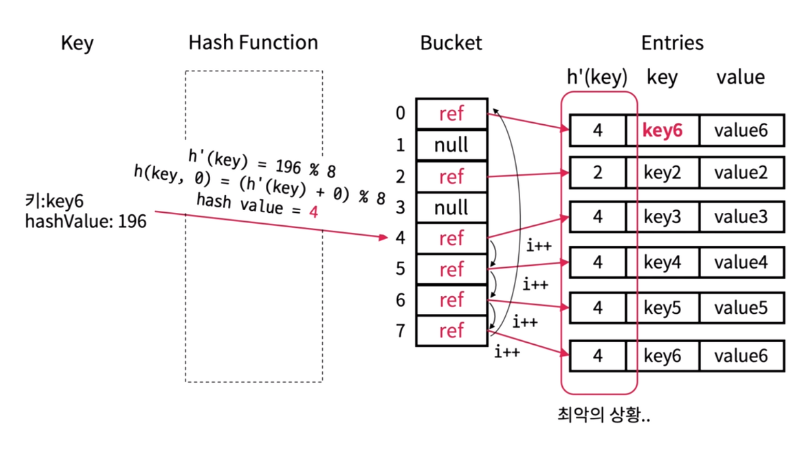
3. 이중 해싱 (Double hashing)
- 탐사할 해시값의 규칙성을 없애서 Clustring(군집화)를 방지하는 기법이다
- 최초의 해시값을 얻는 해시함수, 해시충돌이 일어났을 때 탐사 이동 폭을 얻기 위한 해시함수, 총 두 개의 해시함수를 사용한다
- 해시 충돌의 발생 가능성은 아주 낮아지지만, 추가적인 해시함수 연산이 있어 전체적인 해시테이블에 큰 영향을 미친다
