[PCCP] 시간 복잡도 ( Time Complexity )

▼ Why ?

이번에 프로그래머스에서 진행했던 코딩역량전문인증(PCCP) 대비 특강에서 배운 내용들을 복습하고자 매일 차례차례 정리하고자 한다. 일단 2학년 1학기에도 자료구조 수업에서 배웠던 시간 복잡도에 대해 다시 한 번 알아보는 시간을 가졌다.

---

▼ 시간 복잡도 (Time Complexity)

 

시간 복잡도 ?

• 프로그램의 연산횟수와 연산량,
  즉, 입력값 변화에 따라 연산을 실행할 때, 연산횟수에 비해 시간이 얼마나 걸리는지를 함수 관계로 나타낸 것 !
  
  
• 효율적인 알고리즘을 구현했다 !
  ➜ 입력값이 커짐에 따라 증가하는 시간의 비율을 최소화한 알고리즘을 구성했다

 

시간복잡도를 표현하는 방법

• Big - O
  ➜ 최악의 상황 (Worst case)
  
  
• Big - Ω
  ➜ 최선의 상황 (Best case)
  
  
• Big - Θ
  ➜ 최악과 최선의 평균으로 연산량을 계산하는 표기

 

Big - O

• 시간 복잡도는 주로 Big - O 표기법으로 표현
  ➜ 최악의 경우를 고려해야 프로그램이 실행되는 과정에서 최악의 시간이 소요됐을 때 대응 가능 !

 

Big - O 표기법의 종류

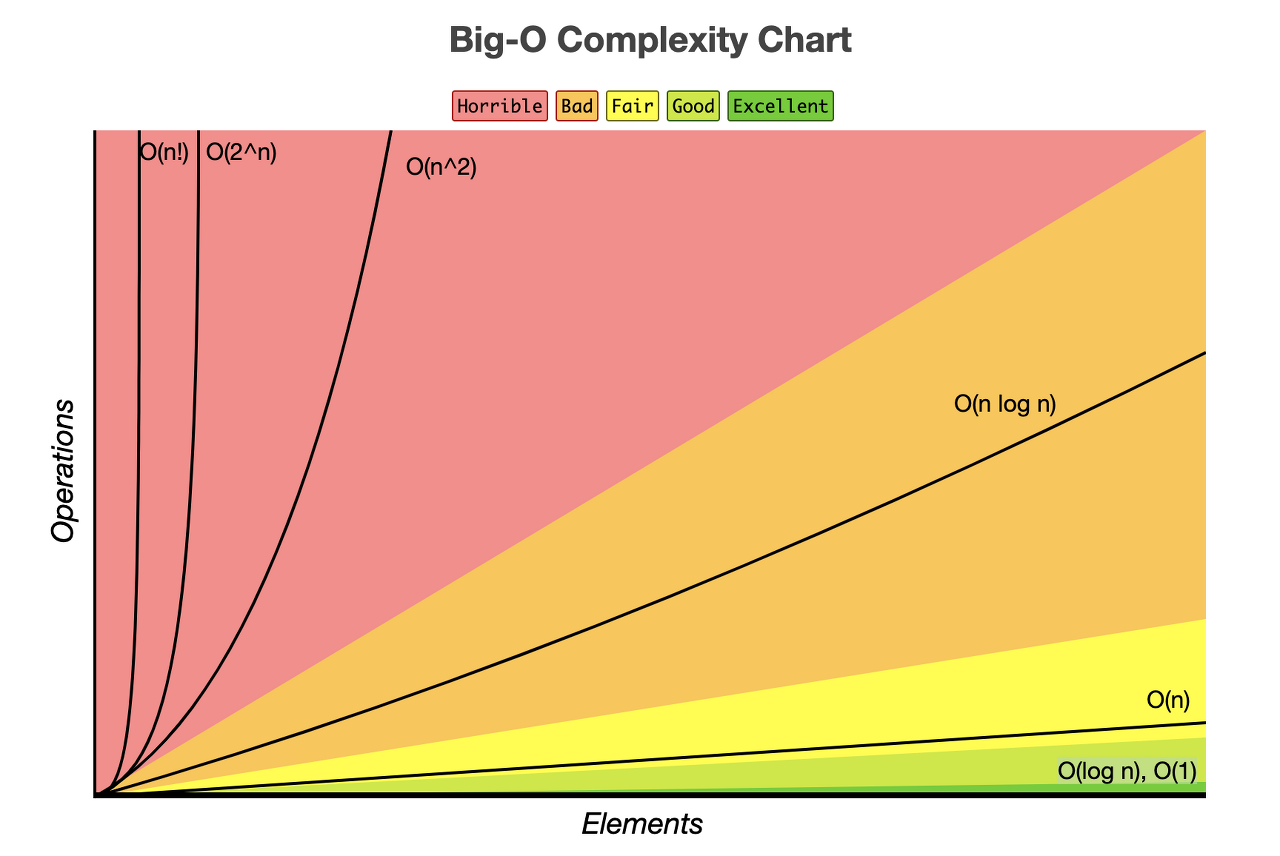
• O(1)
  • 처리해야 할 데이터양(입력값의 크기)와 상관없이 연산량이 항상 일정
    ➜ 입력값이 증가해도 시간이 늘어나지 않는다
    
    
• O(n)
  • 처리해야 할 데이터양 ∝ 연산량
    ➜ 입력값이 증가함에 따라 시간 또한 같은 비율로 증가
  • 효율성을 고려해야 하는 문제는 시간 복잡도가 O(n)이 되도록 코드를 수정하자 !
    ➜ 입력값(n)의 크기가 100,000 이상으로 넘어가면 시간 복잡도가 O(n)이 되도록
    
    
• O(n^2)
  • 처리해야 할 데이터양 ^ 2 ∝ 연산량
    ➜ 입력값이 증가함에 따라 시간이 n이 제곱수의 비율로 증가
    
    
• O(log n)
  • 처리해야 할 데이터양이 증가해도 연산량이 별로 증가 X
    ➜ O(1) 다음으로 빠른 시간 복잡도
    
    
• O(nlogn)
  • 병합 정렬(Merge sort; 분할 정복 기법)
  • 퀵 정렬(Quick sort)
  • 힙 정렬(Heap Sort) - Max/Min Heap