[PCCP] 시뮬레이션 (Simulation) [1]

▼ Why ?

이전 문제 [웅덩이]와 같은 구현(Implementation) - 시뮬레이션(Simulation)  문제이지만, 이전 문제보다는 생각해야 할 부분이 좀 더 추가된 것 같아서 풀어보았다.

---

▼ 안전지대

 

문제 정보

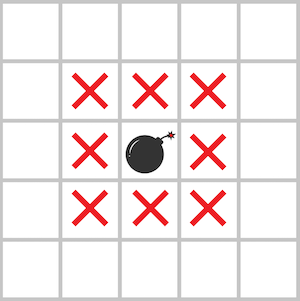
다음 그림과 같이 지뢰가 있는 지역과 지뢰에 인접한 위, 아래, 좌, 우 대각선 칸을 모두 위험지역으로 분류합니다.

지뢰는 2차원 배열 board에 1로 표시되어 있고 board에는 지뢰가 매설 된 지역 1과, 지뢰가 없는 지역 0만 존재합니다.
지뢰가 매설된 지역의 지도 board가 매개변수로 주어질 때, 안전한 지역의 칸 수를 return하도록 solution 함수를 완성해주세요.

코딩테스트 연습 - 안전지대 | 프로그래머스 스쿨 (programmers.co.kr)

프로그래머스

 

제한사항

• board는 n * n 배열입니다.
• 1 ≤ n ≤ 100
• 지뢰는 1로 표시되어 있습니다.
• board에는 지뢰가 있는 지역 1과 지뢰가 없는 지역 0만 존재합니다.

 

입출력 예

 

어떻게 해결해야 할까?

1. 이 문제 또한 제시해준 상황에 따라 구현하기만 하면 되는 문제이다
2. 행렬의 크기가 작아서 완전 탐색(모든 경우의 수를 시도하는 방법)을 해도 될 것 같다
3. 동서남북 4방향이 아닌 주위 8칸을 확인해야 하기 때문에 방향 배열을 북쪽에서부터 시계방향으로 대각선의 방향도 확인할 수 있도록 생성하자
4. 단방향으로 체크하면서 현재 위치의 주위 8칸에 지뢰가 있을 때마다 ' safeSpaceCount ' (안전지대 개수; 초기값 = 2차원 배열의 크기값) 변수의 값에서 1을 빼주자

 

해결 코드 0

• 위에 내용대로 구현하여 문제없이 해결 가능했다

import java.util.*;

public static int solution(int[][] board) {
    int n = board.length;
    int[] dx = {-1, -1, 0, 1, 1, 1, 0, -1};
    int[] dy = {0, 1, 1, 1, 0, -1, -1, -1};
    int safeSpaceCount = n * n;

    for(int i = 0; i < n; i++) {
        for(int j = 0; j < n; j++) {
            if(board[i][j] == 1) {
                safeSpaceCount--;
                continue;
            }

            for(int k = 0; k < 8; k++) {
                int nx = i + dx[k], ny = j + dy[k];
                
                if((nx >= 0 && nx < n) && (ny >= 0 && ny < n) ) {
                    if (board[nx][ny] == 1) {
                        safeSpaceCount--;
                        break;
                    }
                }
            }
        }
    }

    return safeSpaceCount;
}

 

해결 코드 1

1. 위의 방식처럼 주변 8칸에 지뢰가 있는지 체크하는 것이 아닌 다른 방식으로도 해보았다
2. 지뢰가 설치된 위치들을 찾고, 설치된 위치의 주변 8칸에 비안전지대 표시하는 값을 넣는다
3. 안전지대인 곳들만 체크하여 카운트 해준다
4. 이 방식도 완전 탐색이다

import java.util.*;

public static int solution(int[][] board) {
    int[] dx = {-1, -1, 0, 1, 1, 1, 0, -1};
    int[] dy = {0, 1, 1, 1, 0, -1, -1, -1};
    int n = board.length;
    int safeSpaceCount = 0;
    
    for(int i = 0; i < n; i++) {
        for(int j = 0; j < n; j++) {
            if(board[i][j] == 1) {
                for(int k = 0; k < 8; k++) {
                    int nx = i + dx[k]; int ny = j + dy[k];
                    
                    if(nx < 0 || nx >= n || ny < 0 || ny >= n) continue;
                    
                    if(board[nx][ny] == 0) board[nx][ny] = 2;
                }
            }
        }
    }
    
    for(int i = 0; i < n; i++) {
        for(int j = 0; j < n; j++) {
            if(board[i][j] == 0) safeSpaceCount++;
        }
    }
    
    return safeSpaceCount;
}

 

---

▼ 정리

 

• 사실 위의 두 코드 모두 O(n^3)의 시간 복잡도를 갖기 때문에, 시간 복잡도를 최소한으로 줄인 알고리즘은 아니다
  
  ➜ 배열의 크기가 상당히 큰 경우엔 BFS나 DFS를 이용하여 시간 복잡도를 O(n^2) 만큼 줄일 수 있어 성능을 개선시킬 여지는 있지만, 그것을 요구하는 문제는 아닌 것 같아 완전 탐색만으로 풀기에 충분한 문제라고 생각한다