[GDSC] 알고리즘 스터디 3주차 : 힙(Heap)

▼ Why ?

대학 강의 "Data structure" 에서 '우선순위 큐(Priority Queue)'를 구현하기 위해 '힙(Heap)' 이라는 자료구조에 대해 배웠었다. 그리고 "이산수학" 과 "알고리즘" 이라는 강의에선 배운 '허프만 코딩(Huffman coding)' 을 구현하기 위해선 '우선순위 큐' 를 생성해주기 때문에 '힙(Heap)'이라는 자료구조를 이해할 필요가 있었다. 이처럼 '우선순위 큐(Priority Queue)' 는  주로  '최대 힙(Max Heap)' 을 기반으로 구현하게 되는데, 그 이유는 힙(Heap)의 특성상 최대값(Max) 혹은 최소값(Min)을 찾을 때 선형 시간 O(1)이 걸리고 데이터의 삽입 및 삭제 속도도 O(logN) 시간이 소요되기 때문이다. 일반적인 '큐(Queue)' 보다 속도적인 측면에서 더 빠른 '우선순위 큐' 는 '힙 정렬(Heap Sort)', '다익스트라' 알고리즘처럼 다양한 알고리즘에 활용되는 자료구조이기 때문에 매우 중요하다고 할 수 있다. 따라서,  '우선순위 큐' 를 이해하기 위해선 '힙' 에 대한 개념부터 제대로 잡아야 하기 때문에, 자료구조 '힙(Heap)'에 대해 다시 공부해보려고 한다.

---

▼ What ?

3주차엔 힙(Heap)이라는 자료구조에 대해 공부하고 개념을 정리한 다음, 힙을 이용해서 알고리즘 문제도 해결해보려고 한다.  

---

▼ 힙(Heap) & 우선순위 큐(PriorityQueue)

 

힙 (Heap) ?

• 힙(Heap)은 데이터의 최댓값과 최솟값을 빠르게 찾기 위해 고안된 "완전 이진 트리(Complete Binary Tree)" 이다.
  
  완전 이진 트리(Complete Binary Tree) ?
  : 노드가 왼쪽부터 채워지는 트리로, '완전 이진 트리' 는 요소를 배열에 그대로 삽입해주기만 하면 구현할 수 있다 !
  ( 마지막 레벨을 제외하고 모든 레벨이 완전히 채워져 있으며, 마지막 레벨의 모든 노드는 가능한 한 가장 왼쪽에 있다. )

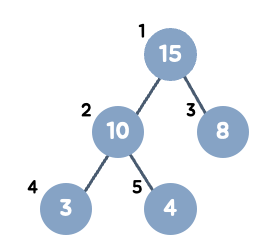
🔻 (부모 노드의 인덱스) = (자식 노드의 인덱스) // 2

    (왼쪽 자식 노드의 인덱스) = (부모 노드의 인덱스) * 2

    (오른쪽 자식 노드의 인덱스) = (부모 노드의 인덱스) * 2 + 1

 

---

 

힙(Heap)의 종류

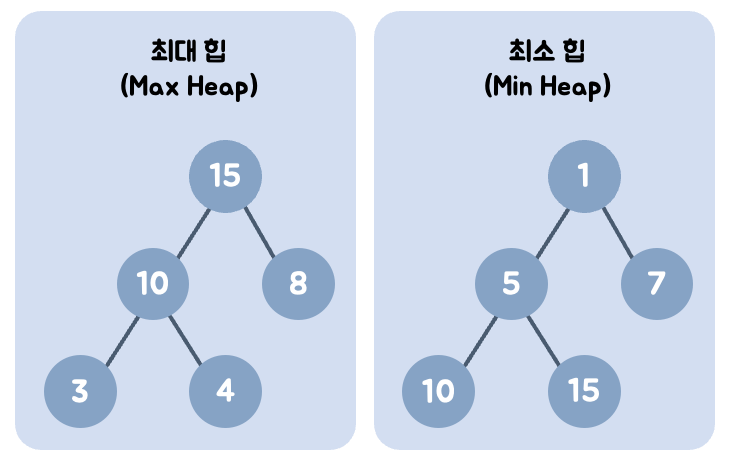
• 힙(Heap)은 두 가지 종류로 나눠질 수 있는데, 하나는 최대 힙(Max Heap), 다른 하나는 최소 힙(Min Heap)이다.
  ➜ 그림에서 알 수 있듯이 '최대 힙' 은 부모 노드가 자식 노드보다 큰 값을 가지고, '최소 힙' 은 반대로 부모 노드가 자식 노드보다 작은 값을 가진다.

 

---

 

힙(Heap)에서의 데이터 삽입 & 삭제 (Heapify)

• 데이터 삽입은 앞서 말했듯이 힙(Heap)은 '완전 이진 트리' 이기 때문에 최하단 노드부터 값을 채운다.
  ➜ (Max Heap) 그 후의 과정은,
  값을 삽입한 후에 부모 노드의 값과 비교하여 부모 노드의 값보다 작으면 그 자리에 두고, 부모 노드의 값보다 크면 부모 노드와 자리를 바꾼다.(swap)
  ➜ Heapify - Sift-up 방식

 

• 데이터 삭제는 앞서 말했던 힙(Heap)의 특성에 따라 항상 루트 노드가 삭제되는데, 해당 노드가 삭제된 이후엔 가장 최하단부 노드를 루트 노드의 자리로 옮긴다.
  ➜ (Max Heap) 그 후의 과정은,
  자식 노드들의 값과 비교를 하여 자식 노드의 값보다 작은 경우엔 자식 노드와 위치를 바꿔준다.(swap)
  만약, 두 자식 노드들이 모두 부모 노드보다 크다면, 두 자식 노드들 중 값이 더 큰 자식 노드와 위치를 바꿔준다.(swap)
  ➜ Heapify - Sift down 방식

 

• 힙 생성 (Heapify) ?
  ➜ 힙에 새로운 요소가 삽입(Sift-up)되거나 기존의 요소가 삭제(Sift-down)될 경우 다시 '최대 힙' 혹은 '최소 힙' 의 조건을 만족하도록 노드의 위치를 바꿔 재구조화하는 과정을 '힙 생성(heapify)' 라고 한다.
  시간 복잡도 ➜  O(logn) (층수만큼 비교)
  
• 힙 자료구조를 구현할 때는 모든 노드를 'heapify' 해줄 필요가 없다 !
  ➜ n/2개 정도의 노드만 'heapify' 해줘도 힙 자료구조가 생성되기 때문에, 힙 자료구조를 구현하는데 소요되는 시간 복잡도는 O(n/2) * O(logn) = O(n)이다 !
  ( 사실상, O(logn)은 O(n/2)보다 작기 때문에 '힙 자료구조' 를 생성하는데 걸리는 시간은 O(n)이라고 한다 ! )
  

 

---

 

힙(Heap) vs 이진 탐색 트리(Binary Search Tree)

• 이진 탐색 트리(Binary Search Tree) = 이진 탐색(Binary Search) + 연결 리스트(Linked-List)
  ➜ 각 노드에서 왼쪽의 자식 노드는 해당 노드(부모)보다 작은 값으로, 오른쪽의 자식 노드는 해당 노드(부모)보다 큰 값으로 구성된다.
  
  
• 힙(Heap)은 왼쪽 노드의 값이 크든 오른쪽 노드의 값이 크든 상관이 없다 !
  
  
• 둘다 "완전 이진 트리" 라는 점은 같다.

 

---

 

힙(Heap)은 왜 사용할까 ?

• 일반적인 배열을 사용하여 최댓값 혹은 최솟값을 찾거나 선형 시간, 즉 O(N)의 시간 복잡도가 요구된다.
  ➜ 힙(Heap) 자료구조를 사용하게 되면 최댓값, 최솟값을 찾아서 제거 후 반환하는 작업뿐만 아니라 새로운 데이터를 삽입하는 작업조차 O(logN)의 시간 복잡도로 줄일 수 있게 된다.
  
  그 이유는 ?
  ➜ 힙(Heap)은 특정 순서에 따라 미리 정렬되어 있다.
  ➜  따라서, '삽입' 과 '삭제(최댓값, 최솟값)' 작업을 수행할 때 생성된 트리의 레벨, 즉 층수(logN)만큼만 비교하면 된다는 점 때문에 O(logN)의 시간밖에 안걸리는 것이다 !
  ( 일반적인 배열에선 모든 값을 비교해야 한다. )
  

 

---

 

우선순위 큐 (PriorityQueue)

• 큐(Queue)처럼 FIFO(First In First Out) 구조를 가지면서, 큐(Queue)와 다르게 들어온 순서대로가 아닌 우선순위에 따라 우선순위가 높은 데이터부터 먼저 나가는 자료구조이다 !
  ➜ 그렇기 때문에, 우선순위 큐(PriorityQueue)는 힙(Heap)을 이용하여 구현하는 것이 일반적인 것 !
  
  
• '우선순위 큐' 를 이용하면 '힙 정렬(Heap Sort)' 도 쉽게 구현 가능하다 !

Heap Sort (참고 자료) - [Algorithm] 버블(Bubble) · 선택(Selection) · 삽입(Insertion) · 쉘(Shell) · 합병(Merge) · 퀵(Quick) · 힙(Heap) 정렬 — Uykm_Note (tistory.com) 

[Algorithm] 버블(Bubble) · 선택(Selection) · 삽입(Insertion) · 쉘(Shell) · 합병(Merge) · 퀵(Quick) · 힙(Heap)

 

• PriorityQueue 객체 생성 (Integer 타입)

PriorityQueue<Integer> pq = new PriorityQueue<>(); // 낮은 숫자가 우선순위인 Integer형 우선순위 큐
PriorityQueue<Integer> reverse_pq = new PriorityQueue<>(Collections.reverseOrder()); // 높은 숫자가 우선순위인 Integer형 우선순위 큐

🔻 낮은 숫자가 우선순위인 우선순위 큐는 'Min Heap' 의 구조를 따른다고 볼 수 있고, 높은 숫자가 우선순위인 우선순위 큐는 'Max Heap' 의 구조를 따른다고 볼 수 있다.

 

• PriorityQueue의 주요 메서드는 아래의 Queue의 메서드와 동일하다
  (추가) Object remove(Object o) : 큐에서 o를 제거
  ➜ 메서드 내부에서 O(n) 만큼의 시간 복잡도를 요구하기 때문에 사용은 지양하자

 

 

참고 자료 - [JAVA] 컬렉션 프레임웍 ( Collections Framework ) — Uykm_Note (tistory.com)

[JAVA] 컬렉션 프레임웍 ( Collections Framework )

---

▼ 이중 우선순위 큐

 

문제 정보

이중 우선순위 큐는 다음 연산을 할 수 있는 자료구조를 말합니다.

이중 우선순위 큐가 할 연산 operations가 매개변수로 주어질 때, 모든 연산을 처리한 후 큐가 비어있으면 [0,0] 비어있지 않으면 [최댓값, 최솟값]을 return 하도록 solution 함수를 구현해주세요.

 

코딩테스트 연습 - 이중우선순위큐 | 프로그래머스 스쿨 (programmers.co.kr)

프로그래머스

 

제한사항

• operations는 길이가 1 이상 1,000,000 이하인 문자열 배열입니다.
• operations의 원소는 큐가 수행할 연산을 나타냅니다.
  • 원소는 “명령어 데이터” 형식으로 주어집니다.- 최댓값/최솟값을 삭제하는 연산에서 최댓값/최솟값이 둘 이상인 경우, 하나만 삭제합니다.
• 빈 큐에 데이터를 삭제하라는 연산이 주어질 경우, 해당 연산은 무시합니다.

 

입출력 예

 

해결 코드 0

• 문제의 제목에서 알 수 있듯이, 우선순위 큐를 사용하면 쉽게 풀 수 있는 문제이다.

1. 우선순위 큐 라이브러리를 사용해서 우선순위 큐 객체를 생성해준다.
2. 입력받은 문자열 배열을 차례대로 주어진 명령어 조건에 맞게 처리해주면 된다.
   • 숫자를 삽입하는 경우엔 별다른 경우를 생각할 필요없이 삽입해주면 된다.
   • 데이터를 삭제해야 하는 경우는 한 가지 고려해야 할 점이 있는데, 앞서 우선순위 객체 'priorityQueue' 를 생성했을 때처럼 별다른 인자 없이 생성했을 경우엔 "Min Heap" 자료구조를 기반으로 작동하기 때문에 숫자가 작을수록 높은 우선순위가 적용된다. 그리고 우선순위가 높은 데이터부터 먼저 나간다는 점 때문에 최솟값을 삭제할 때엔 바로 'remove()' 메서드를 호출해주면 되지만, 최댓값을 삭제해야 할 경우엔 우선순위가 가장 낮은 데이터를 뽑아내야 하기 때문에 추가적인 방법이 필요하다.
     ➜ 최대값이 나올 때까지 데이터를 'poll()' 메서드로 꺼내 따로 생성해둔 임시 배열 'tmp' 에 저장해두고, 최대값을 삭제한 다음에 다시 임시 배열에 저장된 값들을 'priorityQueue' 에 삽입해줬다.
3. 마지막에 우선순위 큐에 저장된 데이터들 중 최댓값과 최솟값을 결과값으로 출력하는 경우도 같은 방식으로 해결하였다.

import java.util.PriorityQueue;

class Solution {
    public int[] solution(String[] operations) {
        int[] answer = new int[2];
        PriorityQueue<Integer> priorityQueue = new PriorityQueue<>();
        
        for(String operation : operations) {
            String[] op = operation.split(" ");
            if(op[0].equals("I")) {
                priorityQueue.offer(Integer.valueOf(op[1]));
            } else if(op[0].equals("D") && !priorityQueue.isEmpty()) {
                if(Integer.parseInt(op[1]) == 1) {
                    Integer[] tmp = new Integer[priorityQueue.size() - 1];
                    int i = 0;
                    
                    while(priorityQueue.size() > 1) {
                        tmp[i++] = priorityQueue.poll();
                    }
                    priorityQueue.remove();
                    
                    for(Integer t : tmp) {
                        priorityQueue.offer(t);
                    }
                } else {
                    priorityQueue.remove();
                }
            }
        }
        
        if(priorityQueue.isEmpty()) return answer;
        
        answer[1] = priorityQueue.poll();
        
        while(priorityQueue.size() > 1) {
            priorityQueue.remove();
        }
        
        answer[0] = priorityQueue.poll();
        
        return answer;
    }
}

 

해결 코드 1

• Min Heap 자료구조를 기반으로 생성한 우선순위 큐에서 최댓값도 뽑아내기 위한 방법으로 임시배열을 따로 생성했던 탓에 이중 for문을 사용하여 O(n^2)의 시간 복잡도가 나타났다.
  ➜ 다시 생각해보니 굳이 'Min Heap' 을 기반으로 생성하여 최솟값을 먼저 내보내는 우선순위 큐 객체에서 최댓값도 탐색할 필요가 없었던 것 같다.

1. 'Max Heap' 을 기반으로 하는 우선순위 큐 객체 'reverse_pq' 도 추가로 생성해서 최댓값을 삭제하는 연산을 이  객체에서 따로 처리해주자.
   ➜  'Collection.reverseOrder()' 를 정렬 기준값으로 인자에 전달해주면 'Max Heap' 을 기반으로 하는 우선순위 큐 객체를 생성 가능하다.
2. 'remove(int i)' 메서드를 이용해서 'maxQueue' 와 'minQueue' 를 동기화시켜주자

import java.util.PriorityQueue;
import java.util.Collections;

class Solution {
    public int[] solution(String[] operations) {
        int[] answer = new int[2];
        PriorityQueue<Integer> maxQueue = new PriorityQueue<>(Collections.reverseOrder()); // 최대값을 뺄 수 있는 우선순위 큐
        PriorityQueue<Integer> minQueue = new PriorityQueue<>(); // 최소값을 뺄 수 있는 우선순위 큐

        for (String operation : operations) {
            String[] op = operation.split(" ");
            if (op[0].equals("I")) {
                int value = Integer.valueOf(op[1]);
                maxQueue.offer(value);
                minQueue.offer(value);
            } else if (op[0].equals("D") && !maxQueue.isEmpty() && !minQueue.isEmpty()) {
                if (Integer.parseInt(op[1]) == 1) {
                    int max = maxQueue.poll();
                    minQueue.remove(max);
                } else {
                    int min = minQueue.poll();
                    maxQueue.remove(min);
                }
            }
        }

        if (!maxQueue.isEmpty()) {
            answer[0] = maxQueue.poll();
            answer[1] = minQueue.poll();
        }

        return answer;
    }
}

 

---

▼ 정리

 

• 데이터에서 최솟값이나 최댓값을 뽑아내야 하는 경우엔 가장 효율적인 시간 복잡도(logN)로 작업할 수 있는 자료구조 "힙(Heap)" 을 떠올리자.
  
  
• 이번에 시간 복잡도를 리팩토링을 해본 코드와 원래 코드와의 실행 시간을 살펴봤더니 별 차이가 없었다. 그 이유를 알아보았더니 직관적으로 봤을 때 이중 for문을 제거하기 위해 'remove(int element)' 메서드를 사용했는데, 이 메서드 자체가 내부적으로 O(n)의 시간 복잡도를 요구한다는 사실을 알게 되었다.
  ( 오히려 삽입과 삭제 연산에 있어서 효율적인 작업을 수행하기 위해 우선순위 큐를 사용하는 것인데, 이러한 취지에 어긋나는 해결 방법이라고 할 수 있다 ! )
  ➜ 따라서, 라이브러리에서 제공하는 메서드를 사용할 때 해당 메서드 자체의 내부적인 구현 내용을 고려해야 할 필요가 있다는 것을 기억하자 !